
Hyperspectral camera
The main design goal for this one is to have an imaging system that can accept a commercial lens as the imaging lens and perform a hyperspectral sweep. I have both scientific and artistic plans for this camera, so it needed both spatial and spectral resolution.
Overview
This camera operates by masking out a line in the focal plane of the imaging lens. The beam is then collimated by a lens into a diffraction grating. Then a normal camera with a fairly long lens captures the diffracted line. A linear motion stage is then used to sweep the mask across the plane of the imaging lens to aquire the whole image.
Simulations
I didn't feel like going through the hassle of setting up a full optical sim, so instead I wrote a short python script that performed a small 2D ray trace with ideal thin lens and diffraction grating. I wanted to make sure the linear sweep stage kept the spectrum created by the diffration grating to remain in the same place on the camera sensor.
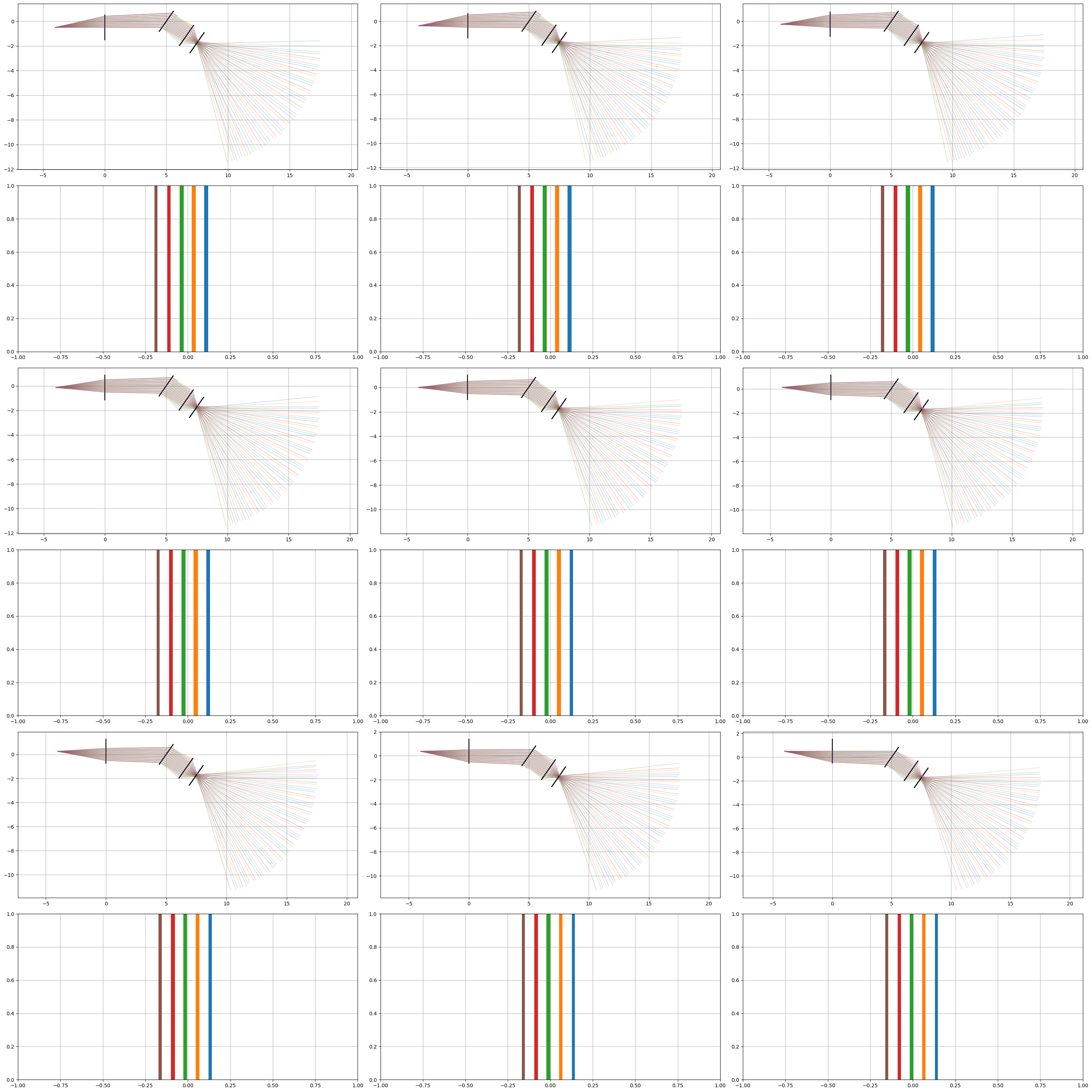
The upper plot is the ray trace and the bottom is the simulated image on the camera sensor.
Linear stage
The line mask needed to be move across the focal plane at a very high resolution. To achieve this I used a linear motor. It consists of a coil of wire sitting in a magnet cage similar to hard drive head motors. The linear motion is constraint with the use of a pair of flextures. I have found that both the mask and the collimating lens have to be mounted to the linear motion stage to ensure the spectrum stay in the same position on the camera sensor as we sweep the focal plane.
To control the linear motor, I used the PWM from the raspberry pi to drive a full bridge.

Sample result
The scene below is a white card with a few different markers drawn on it, illuminated by an incandescent light.
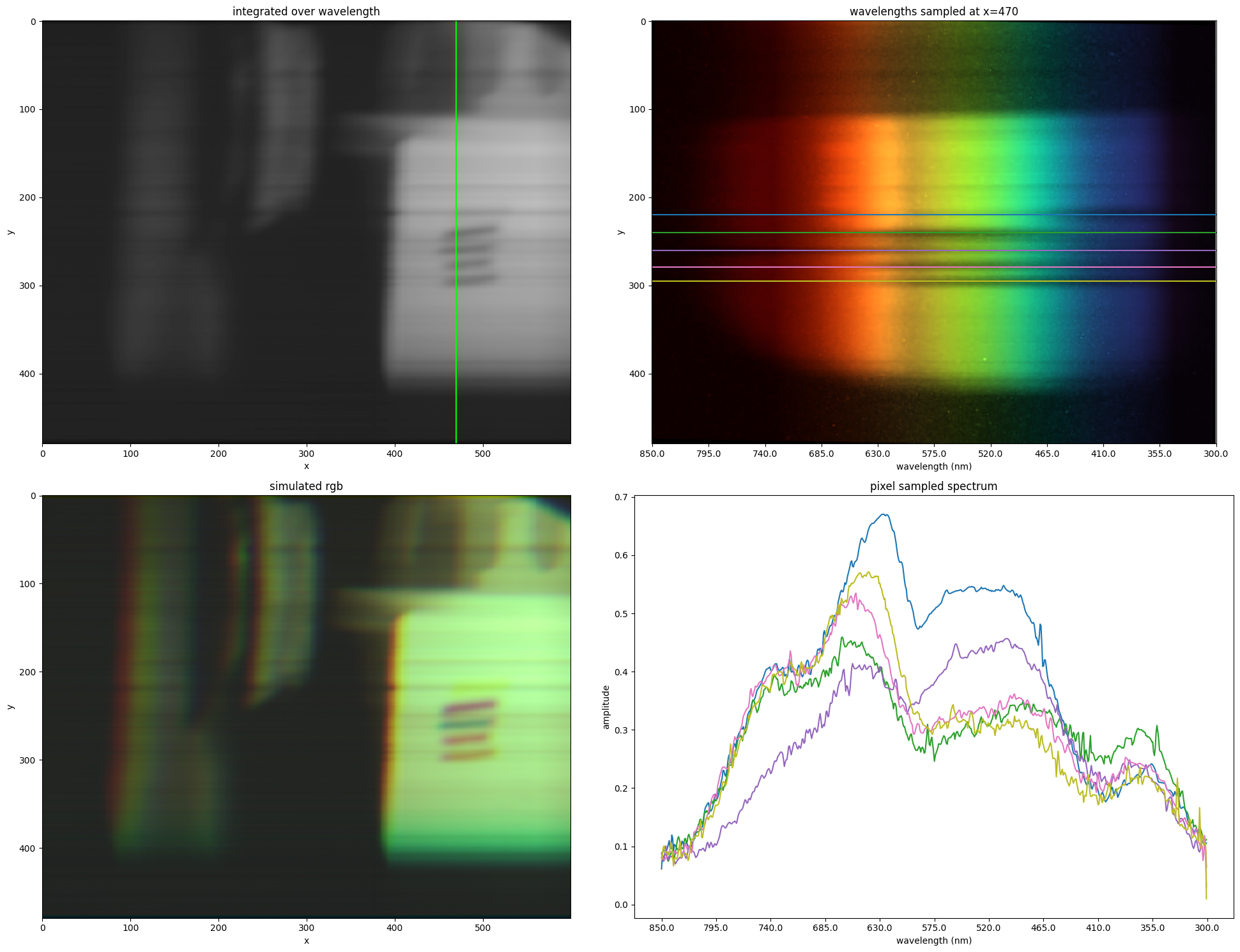
- Top left: iamge of the scene where the intensity of the pixel is the sum of all the spectrum
- Top right: the image as would be seen by the camera sensor at the line indicated in green on the top left image.
- Bottom left: False color by using 3 color bands to approximate a RGB image
- Bottom right: the spectrums of the corresponding lines in the top right image.